ML Optimization; A Primer

TL;DR: Every time you train a neural network, you’re solving an optimization problem in a space with millions of dimensions. This is the story of how we went from basic SGD taking baby steps to Adam’s intelligent adaptive learning—and why choosing the right optimizer can make or break your model.

These paper reviews are written more for me and less for others. LLMs have been used in formatting!

The Mountain Climbing Problem: Why Optimization is Hard

Imagine Being Lost in the Dark

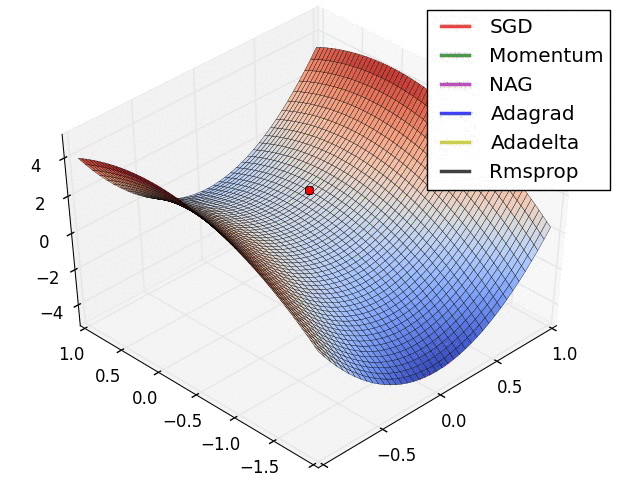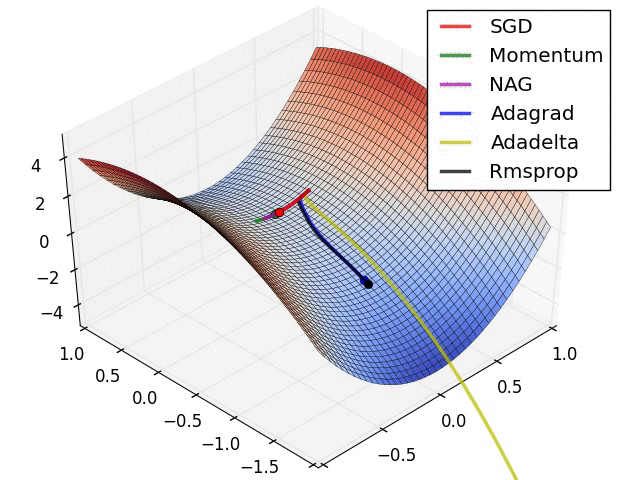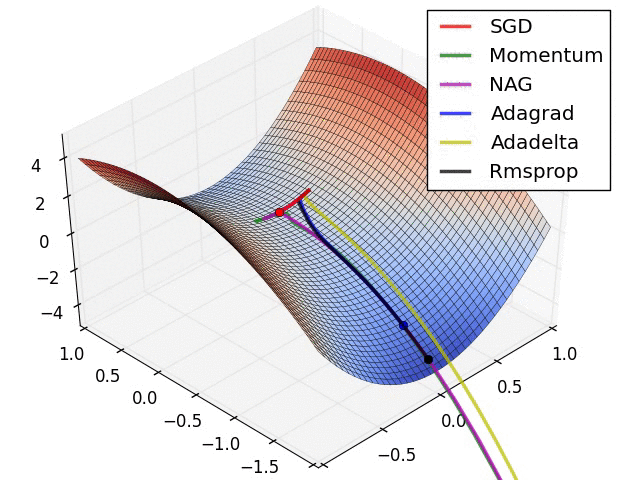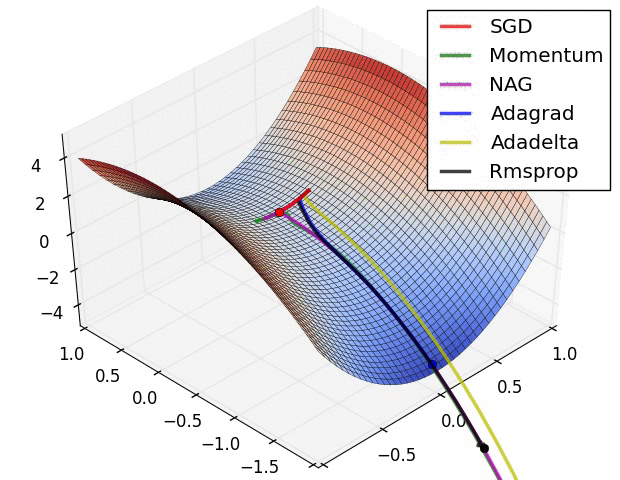
Picture yourself on a mountainous landscape at night, trying to find the lowest valley with only a flashlight. You can see the immediate slope under your feet, but the entire terrain is invisible. This is exactly what neural network optimization looks like.

The challenge:

• Millions of parameters = millions of dimensions
• No global view = only local gradient information
• Multiple valleys = many local minima to get trapped in
• Noisy terrain = stochastic gradients from mini-batches

flowchart LR
   A[Random Start] --> B[Compute Gradient] --> C[Step Down] --> D{Converged?}
   D -->|No| B
   D -->|Yes| E[Found Minimum ✓]
   
   style A fill:#e53e3e,color:#fff
   style B fill:#3182ce,color:#fff
   style C fill:#dd6b20,color:#fff
   style D fill:#38a169,color:#fff
   style E fill:#38a169,color:#fff

The Classical Methods Hit a Wall

Newton’s Method uses second-order information (curvature): \(\theta_{t+1} = \theta_t - H^{-1} \nabla J(\theta_t)\)

Perfect in theory, impossible in practice:

• Computing the Hessian $H$ for millions of parameters?
• Inverting it?
• Storage requirements?

The Revolution: What if we don’t need perfect information? What if good enough gradients from small batches could guide us to excellent solutions?

---

SGD: The Foundation That Changed Everything

The Breakthrough Insight

Instead of using the entire dataset to compute gradients:

\[\nabla J(\theta) = \frac{1}{N} \sum_{i=1}^{N} \nabla J_i(\theta)\]

Stochastic Gradient Descent uses random mini-batches:

\[\theta_{t+1} = \theta_t - \eta \nabla J_{\text{batch}}(\theta_t)\]

Why this works (the statistical magic):

• Each mini-batch gradient is an unbiased estimator of the true gradient
• The noise actually helps escape sharp minima
• Computational cost becomes independent of dataset size

The Mini-Batch Sweet Spot

graph LR
   A[Batch Size 1<br/>Very Noisy] --> B[Batch Size 32<br/>Good Balance]
   B --> C[Batch Size 256<br/>Smooth Progress]
   C --> D[Full Batch<br/>Expensive]
   
   style A fill:#e53e3e,color:#fff
   style B fill:#38a169,color:#fff
   style C fill:#3182ce,color:#fff
   style D fill:#d69e2e,color:#000

The Goldilocks principle:

• Too small: Noisy, erratic updates
• Too large: Expensive, may get stuck
• Just right: 32-256 examples usually optimal

SGD’s Fundamental Limitations

The Narrow Valley Problem:

graph TD
   A[SGD in Narrow Valley] --> B[Step Down Steep Wall]
   B --> C[Overshoot to Other Wall]
   C --> D[Oscillate Back and Forth]
   D --> E[Slow Progress Down Valley]
   
   style A fill:#3182ce,color:#fff
   style B fill:#dd6b20,color:#fff
   style C fill:#dd6b20,color:#fff
   style D fill:#e53e3e,color:#fff
   style E fill:#d69e2e,color:#000

1. Learning rate sensitivity: Too high → divergence, too low → crawling
2. Uniform treatment: Same learning rate for all parameters
3. Ravine oscillations: Bounces between steep walls instead of following the valley

---

Momentum: Adding Physics to Optimization

The Ball Rolling Down a Hill

Key insight: Treat parameter updates like physics—build up velocity over time.

\[v_t = \beta v_{t-1} + \eta \nabla J(\theta_t)\] \[\theta_{t+1} = \theta_t - v_t\]

Physical intuition:

• $v_t$ is velocity (momentum term)
• $\beta$ is friction (typically 0.9)
• Gradients apply force to change velocity

Why Momentum Works Magic

Acceleration in Consistent Directions:

graph LR
   A[Consistent Gradient Direction] --> B[Velocity Builds Up]
   B --> C[Faster Progress]
   
   style A fill:#3182ce,color:#fff
   style B fill:#dd6b20,color:#fff
   style C fill:#38a169,color:#fff

Damping Oscillations:

graph LR
   A[Oscillating Gradients] --> B[Opposing Velocities Cancel]
   B --> C[Smoother Path]
   
   style A fill:#e53e3e,color:#fff
   style B fill:#dd6b20,color:#fff
   style C fill:#38a169,color:#fff

Nesterov’s Lookahead Trick

Standard momentum: Look at current position, then step Nesterov momentum: Look ahead, then decide

\[v_t = \beta v_{t-1} + \eta \nabla J(\theta_t - \beta v_{t-1})\]

Result: Better convergence properties, especially near the minimum.

The Momentum Evolution

Method	Formula	Key Benefit	Limitation
SGD	$\theta \leftarrow \theta - \eta \nabla J$	Simple, reliable	Slow, oscillates
Momentum	$v \leftarrow \beta v + \eta \nabla J$	Faster, smoother	Still uniform LR
Nesterov	Lookahead gradient	Better near minimum	More complex

---

AdaGrad: The First Adaptive Revolution

The Eureka Moment

What if different parameters need different learning rates?

AdaGrad’s insight: Parameters with large historical gradients should get smaller learning rates.

\[G_t = G_{t-1} + \nabla J(\theta_t)^2\] \[\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{G_t + \epsilon}} \nabla J(\theta_t)\]

Why Adaptive Learning Rates Work

The Sparse Data Problem:

graph LR
   subgraph Frequent ["Frequent Words"]
       A[the, and] --> B[Large Gradients] --> C[Smaller LR]
   end
   
   subgraph Rare ["Rare Words"]
       D[serendipity] --> E[Small Gradients] --> F[Larger LR]
   end
   
   style C fill:#e53e3e,color:#fff
   style F fill:#38a169,color:#fff

In NLP contexts:

• Common words appear frequently → accumulate large $G_t$ → get smaller updates
• Rare words appear seldom → small $G_t$ → get larger updates when they do appear
• Result: Balanced learning across vocabulary

AdaGrad’s Fatal Flaw

The Monotonic Accumulation Problem:

\[G_t = G_{t-1} + \nabla J(\theta_t)^2 \quad \text{(only grows, never shrinks)}\]

The death sentence: Eventually, $\frac{\eta}{\sqrt{G_t}} \rightarrow 0$ for all parameters.

---

RMSProp: The Elegant Fix

Forgetting the Distant Past

Hinton’s insight: Use exponential moving average instead of accumulating everything.

\[G_t = \beta G_{t-1} + (1-\beta) \nabla J(\theta_t)^2\]

The magic of exponential decay:

• Recent gradients get weight $(1-\beta)$
• Gradients from $k$ steps ago get weight $(1-\beta)\beta^k$
• Old gradients fade away gracefully

Mathematical insight:

\[\lim_{t \rightarrow \infty} G_t^{\text{AdaGrad}} = \infty\] \[\lim_{t \rightarrow \infty} G_t^{\text{RMSProp}} = \text{bounded}\]

The Practical Success Story

RMSProp became popular not through academic papers, but through Geoffrey Hinton’s Coursera course—a testament to its practical effectiveness over theoretical elegance.

---

Adam: The Convergence of Ideas

Best of All Worlds

Adam combines momentum (first moment) with RMSProp (second moment):

\[m_t = \beta_1 m_{t-1} + (1-\beta_1) \nabla J(\theta_t) \quad \text{(momentum)}\] \[v_t = \beta_2 v_{t-1} + (1-\beta_2) \nabla J(\theta_t)^2 \quad \text{(RMSProp)}\]

The Bias Correction Breakthrough

The early training problem:

• Both $m_t$ and $v_t$ start at zero
• Early estimates are biased toward zero
• Without correction: tiny steps initially

The solution: \(\hat{m}_t = \frac{m_t}{1 - \beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t}\)

Final update: \(\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t\)

Bias Correction Visualization

Iteration	$1-\beta_1^t$	$1-\beta_2^t$	Effect
$t=1$	$0.1$	$0.001$	Huge correction
$t=10$	$0.65$	$0.01$	Moderate correction
$t=100$	$0.99997$	$0.63$	Minimal correction
$t→∞$	$1.0$	$1.0$	No correction needed

The beautiful result: Adam takes appropriately-sized steps from iteration 1, not after a “warm-up” period.

Why Adam Became King

The quadruple advantage:

1. ✅ Momentum for smooth progress
2. ✅ Adaptive learning rates per parameter
3. ✅ Bias correction for good early steps
4. ✅ Robust defaults that work across problems

Default hyperparameters that just work:

• $\beta_1 = 0.9$ (momentum decay)
• $\beta_2 = 0.999$ (second moment decay)
• $\eta = 0.001$ (learning rate)
• $\epsilon = 10^{-8}$ (numerical stability)

---

AdamW: The Weight Decay Fix

The Subtle but Critical Problem

Standard Adam with L2 regularization: \(\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} (\hat{m}_t + \lambda \theta_t)\)

The issue: Weight decay gets scaled by the adaptive learning rates, causing inconsistent regularization.

Decoupled Weight Decay

AdamW’s fix: \(\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t - \eta \lambda \theta_t\)

Key difference: Weight decay is separated from gradient-based updates.

Why This Matters for Large Models

graph TD
   A[Large Model Training] --> B{Weight Decay Method}
   B -->|Adam + L2| C[Inconsistent Regularization]
   B -->|AdamW| D[Proper Regularization]
   C --> E[Potential Overfitting]
   D --> F[Better Generalization]
   
   style A fill:#3182ce,color:#fff
   style B fill:#dd6b20,color:#fff
   style C fill:#d69e2e,color:#000
   style D fill:#d69e2e,color:#000
   style E fill:#e53e3e,color:#fff
   style F fill:#38a169,color:#fff

Impact: AdamW became the optimizer behind most state-of-the-art language models (GPT, BERT, etc.).

---

The Optimizer Family Tree

graph TD
   A[Classical Methods<br/>Newton, Conjugate Gradient] --> B[Scale Problems]
   B --> C[SGD 1951<br/>Stochastic Revolution]
   C --> D[SGD + Momentum 1964<br/>Physics Inspiration]
   C --> E[AdaGrad 2011<br/>Adaptive Learning Rates]
   E --> F[RMSProp 2012<br/>Fixes Dying Learning]
   D --> G[Adam 2014<br/>Combines Everything]
   F --> G
   G --> H[AdamW 2017<br/>Better Weight Decay]
   
   style A fill:#3182ce,color:#fff
   style B fill:#d69e2e,color:#000
   style C fill:#e53e3e,color:#fff
   style D fill:#dd6b20,color:#fff
   style E fill:#dd6b20,color:#fff
   style F fill:#dd6b20,color:#fff
   style G fill:#38a169,color:#fff
   style H fill:#38a169,color:#fff

---

Learning Rate Scheduling: The Temporal Dimension

Why Constant Rates Aren’t Optimal

The training phases:

1. Early: Large steps to find good regions quickly
2. Middle: Moderate steps for steady progress
3. Late: Small steps for fine-tuning

Popular Scheduling Strategies

Step Decay: \(\eta_t = \eta_0 \times \gamma^{\lfloor t/s \rfloor}\)

Cosine Annealing: \(\eta_t = \eta_{\min} + \frac{\eta_{\max} - \eta_{\min}}{2}(1 + \cos(\frac{\pi t}{T}))\)

Warmup + Decay:

graph LR
   A[Linear Warmup<br/>0 → η_max] --> B[Cosine Decay<br/>η_max → η_min]
   
   style A fill:#dd6b20,color:#fff
   style B fill:#3182ce,color:#fff

The Warmup Phenomenon

Why warmup helps large models:

• Random initialization → gradients can be very large/small
• Gradual LR increase → optimizer finds good initial direction
• Prevents early instability in large batch training

---

The Modern Optimization Landscape

When to Use What: The Decision Matrix

Scenario	Recommended Optimizer	Learning Rate	Schedule	Why
Getting Started	AdamW	0.001	Cosine	Robust defaults
Computer Vision	SGD + Momentum	0.01-0.1	Step decay	Often better final accuracy
NLP/Transformers	AdamW	1e-4 to 5e-4	Warmup + decay	Field standard
RNNs/LSTMs	Adam/RMSProp	0.001	Reduce on plateau	Handles gradients well
Limited Compute	SGD + Momentum	0.01	Step decay	Lower memory overhead

Performance Comparison Matrix

Optimizer	Speed	Memory	Robustness	Final Quality	Best For
SGD	⭐⭐⭐	⭐⭐⭐	⭐⭐	⭐⭐⭐	CV, when tuned well
Momentum	⭐⭐⭐	⭐⭐⭐	⭐⭐⭐	⭐⭐⭐	Most CV tasks
AdaGrad	⭐⭐	⭐⭐	⭐⭐	⭐⭐	Sparse data, short runs
RMSProp	⭐⭐	⭐⭐	⭐⭐⭐	⭐⭐⭐	RNNs, non-stationary
Adam	⭐⭐	⭐⭐	⭐⭐⭐⭐	⭐⭐⭐	General purpose
AdamW	⭐⭐	⭐⭐	⭐⭐⭐⭐	⭐⭐⭐⭐	Large models, NLP

---

Debugging Training: The Troubleshooting Guide

Loss Patterns and Solutions

graph TD
   A[Training Issues] --> B{Loss Pattern}
   B -->|Exploding| C[Lower LR, Gradient Clipping]
   B -->|Not Decreasing| D[Higher LR, Different Optimizer]
   B -->|Oscillating| E[Lower LR, Add Momentum]
   B -->|Plateauing| F[LR Schedule, Different Architecture]
   
   style A fill:#3182ce,color:#fff
   style B fill:#dd6b20,color:#fff
   style C fill:#e53e3e,color:#fff
   style D fill:#d69e2e,color:#000
   style E fill:#3182ce,color:#fff
   style F fill:#38a169,color:#fff

The Hyperparameter Hierarchy

Priority order for tuning:

1. Learning Rate (biggest impact, tune first)
2. Batch Size (affects dynamics and memory)
3. Learning Rate Schedule (can dramatically improve convergence)
4. Optimizer Choice (try Adam/AdamW first, then SGD)
5. Optimizer Parameters (usually keep defaults)

---

The Philosophical Impact

What Optimization Taught Us About Learning

Key insights from the optimization journey:

1. 🚀 Noise can be beneficial (SGD’s stochastic nature helps escape bad minima)
2. 📈 Adaptation beats fixed rules (adaptive learning rates outperform constant ones)
3. 🔄 History matters (momentum and moving averages provide crucial context)
4. ⚖️ Balance is key (trade-offs between speed, stability, and final quality)

The Meta-Lesson

Optimization isn’t just about math—it’s about understanding the learning process itself.

The evolution from SGD to Adam mirrors how we learn:

• Start with big, exploratory steps
• Build momentum when making progress
• Adapt based on experience
• Fine-tune as we approach mastery

---

Implementation Deep Dive

PyTorch Quick Reference

# The essentials
import torch.optim as optim

# SGD with momentum (CV standard)
optimizer = optim.SGD(model.parameters(), 
                     lr=0.01, momentum=0.9, weight_decay=1e-4)

# Adam (general purpose)
optimizer = optim.Adam(model.parameters(), 
                      lr=0.001, betas=(0.9, 0.999))

# AdamW (modern default)
optimizer = optim.AdamW(model.parameters(), 
                       lr=0.001, weight_decay=0.01)

# With scheduling
scheduler = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=epochs)

The Training Loop Template

for epoch in range(epochs):
    for batch in dataloader:
        # Forward pass
        outputs = model(batch.x)
        loss = criterion(outputs, batch.y)
        
        # Backward pass
        optimizer.zero_grad()  # Clear gradients
        loss.backward()        # Compute gradients
        
        # Optional: gradient clipping
        torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
        
        optimizer.step()       # Update parameters
    
    scheduler.step()          # Update learning rate

---

Empirical Wisdom: What Really Works

The 80/20 Rules

80% of optimization success comes from:

1. ✅ Choosing the right learning rate
2. ✅ Using a learning rate schedule
3. ✅ Picking AdamW for most problems
4. ✅ Adding warmup for large models

The remaining 20%:

• Fine-tuning momentum/beta parameters
• Specialized optimizers for specific domains
• Advanced techniques like gradient clipping
• Problem-specific architectural choices

Battle-Tested Configurations

Computer Vision (ResNet/EfficientNet):

optimizer = optim.SGD(lr=0.1, momentum=0.9, weight_decay=1e-4)
scheduler = optim.lr_scheduler.StepLR(step_size=30, gamma=0.1)

Transformers (BERT/GPT style):

optimizer = optim.AdamW(lr=5e-4, weight_decay=0.01)
# Warmup for 10% of steps, then linear decay

RNNs/LSTMs:

optimizer = optim.Adam(lr=0.001)
scheduler = optim.lr_scheduler.ReduceLROnPlateau(patience=5)

---

Conclusion: The Optimization Odyssey

The Journey We’ve Taken

From SGD’s simple steps to Adam’s adaptive intelligence, we’ve witnessed a 40-year evolution in how machines learn:

timeline
    title The Optimization Timeline
    1951 : SGD
         : Stochastic revolution begins
    1964 : Momentum
         : Physics meets optimization
    2011 : AdaGrad
         : Adaptive learning rates
    2012 : RMSProp
         : Fixing the learning death
    2014 : Adam
         : The convergence of ideas
    2017 : AdamW
         : Perfecting weight decay
    2025 : Future
         : Learned optimizers?

The Meta-Insights

What optimization taught us about machine learning:

1. 🎯 Simple ideas scale: SGD’s basic concept still powers trillion-parameter models
2. 🔄 Iteration beats perfection: Practical improvements matter more than theoretical optimality
3. 📊 Empirical validation rules: What works in practice often surprises theory
4. ⚖️ Trade-offs are everywhere: Speed vs. stability, simplicity vs. performance

The Practical Truth

For most practitioners today:

• Start with AdamW and cosine annealing
• Tune learning rate first, everything else second
• Use warmup for large models or large batch sizes
• Try SGD+momentum for computer vision if you have time
• Focus on architecture and data more than optimizer tweaking

Looking Forward

The field keeps evolving. Future directions:

• Learned optimizers that adapt to your specific problem
• Distributed optimization for models too large for single machines
• Problem-aware optimization that understands your domain
• Meta-learning approaches that learn how to learn

The eternal truth: No matter how sophisticated our optimizers become, the fundamental challenge remains the same—navigating high-dimensional landscapes toward better solutions, one step at a time.

---

Further Reading & References

Foundational Papers

• SGD: Robbins & Monro (1951) - The original stochastic approximation
• Momentum: Polyak (1964) - Heavy ball method
• AdaGrad: Duchi et al. (2011) - Adaptive subgradient methods
• Adam: Kingma & Ba (2014) - Adam: A method for stochastic optimization
• AdamW: Loshchilov & Hutter (2017) - Decoupled weight decay regularization

---

Happy optimizing! 🎯