The Paper That Started the Neural NLP Revolution: Bengio's Neural Probabilistic Language Model

Posted Jan 17, 2025 Updated Jun 28, 2025

Neural Language Model Architecture

By Abu Shahid

8 min read

The Paper That Started the Neural NLP Revolution: Bengio's Neural Probabilistic Language Model

TL;DR: Yoshua Bengio’s 2003 paper “A Neural Probabilistic Language Model” is the Genesis of modern NLP. Before this paper, language models were statistical counting machines. After it, they became neural networks that could learn distributed representations of words. This work laid the groundwork for everything from Word2Vec to GPT.

These paper reviews are written more for me and less for others. LLMs have been used in formatting

The Problem: Traditional Language Models Hit a Wall

The Curse of Dimensionality in Language

Imagine you’re trying to predict the next word in a sentence. Traditional n-gram models (think trigrams, 4-grams) worked like this:

\[P(\text{word}_t | \text{word}_{t-1}, \text{word}_{t-2}) = \frac{\text{Count}(\text{word}_{t-2}, \text{word}_{t-1}, \text{word}_t)}{\text{Count}(\text{word}_{t-2}, \text{word}_{t-1})}\]

The fundamental problems:

🕳️ Sparsity: Most n-grams never appear in training data
🚫 No generalization: “The cat is running” tells us nothing about “The dog is running”
💾 Storage explosion: Need to store counts for every possible n-gram combination
❌ Zero probability: Unseen n-grams get probability 0, breaking the model

The Band-Aid Solutions

Techniques like Kneser-Ney smoothing tried to fix this by redistributing probability mass:

Kneser-Ney Insight: Instead of just counting frequency, ask “How likely is a word to appear in novel contexts?”
“Francisco” appears often, but only after “San”
“Kong” appears less, but in diverse contexts (“Hong Kong”, “King Kong”)
For novel contexts, “Kong” is more likely than “Francisco”

But these were still fundamentally limited by treating words as discrete, unrelated symbols.

Bengio’s Breakthrough: Words as Geometry

The Revolutionary Insight

What if words weren’t discrete symbols but points in a continuous vector space where semantically similar words are close together?

This single insight changed everything. Instead of:

cat = symbol_1247
dog = symbol_2891

We get:

cat = [0.2, -0.8, 0.5, ..., 0.1]  # 50-dimensional vector
dog = [0.3, -0.7, 0.4, ..., 0.2]  # Close to cat in vector space!

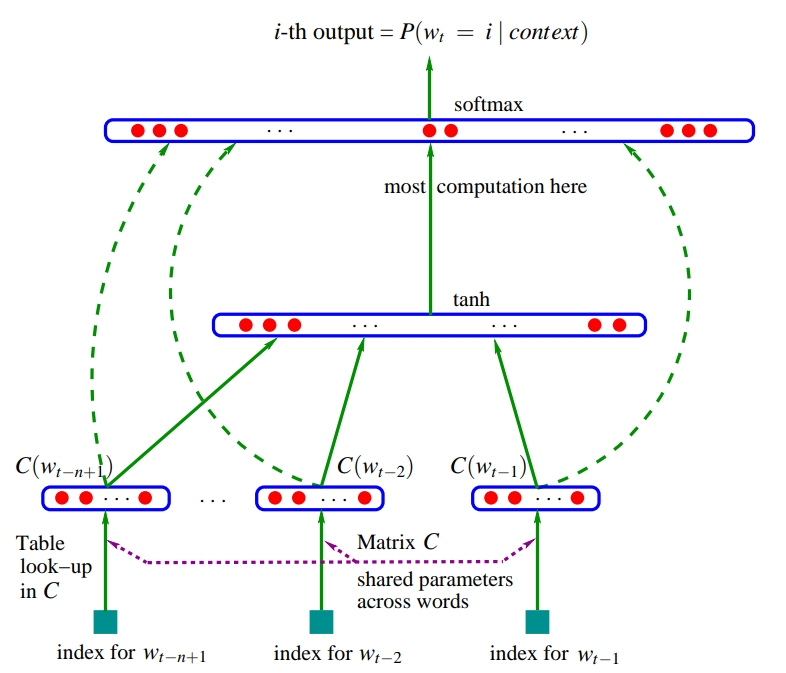
The Architecture That Changed NLP

graph LR
    A[Input: word indices<br/>w₁, w₂, w₃] --> B[Word Embeddings<br/>e₁, e₂, e₃]
    B --> C[Concatenate<br/>Context Vector]
    C --> D[Hidden Layer<br/>tanh activation]
    D --> E[Output Layer<br/>Linear transform]
    E --> F[Softmax<br/>Probability distribution]
    
    style A stroke:#4a90e2,stroke-width:2px
    style B stroke:#7ed321,stroke-width:2px
    style C stroke:#f5a623,stroke-width:2px
    style D stroke:#d0021b,stroke-width:2px
    style E stroke:#9013fe,stroke-width:2px
    style F stroke:#50e3c2,stroke-width:2px

The Mathematical Flow:

Input: Sequence of word indices $[w_{t-n+1}, …, w_{t-1}]$
Embeddings: $[e(w_{t-n+1}), …, e(w_{t-1})] \in \mathbb{R}^{(n-1) \times m}$
Concatenation: $x = [e(w_{t-n+1}); …; e(w_{t-1})] \in \mathbb{R}^{(n-1)m}$
Hidden Layer: $h = \tanh(Wx + b) \in \mathbb{R}^h$
Output: $y = Uh + d \in \mathbb{R}^{\lvert V \rvert}$
Probabilities: $P(w_t \mid \text{context}) = \text{softmax}(y)$

Why This Architecture Was Brilliant

1. Solving the Curse of Dimensionality

Traditional approach:

Need to see every possible n-gram
Parameters grow exponentially with vocabulary

Neural approach:

Learn continuous representations
Interpolate between seen examples
Parameters grow linearly with vocabulary

2. Automatic Feature Discovery

The network automatically learns:

Syntactic features: Verbs cluster together, nouns cluster together
Semantic features: Animals, colors, actions form natural groups
Compositional structure: “running” is close to “run” + temporal marker

3. The Magic of Generalization

If the model learns:

“The cat is sleeping”
“The dog is barking”

It can generalize to:

“The cat is barking” (syntactically valid)
“The dog is sleeping” (makes perfect sense)

Technical Deep Dive

The Embedding Magic

Each word $w$ gets mapped to a learned vector $e(w) \in \mathbb{R}^m$:

\[\text{embedding_matrix}[w] = [e_1, e_2, ..., e_m]\]

Why this works:

Similar words get similar vectors through backpropagation
Geometric relationships emerge: $\text{king} - \text{man} + \text{woman} \approx \text{queen}$
Generalization: “cat runs” helps with “dog runs”

The Neural Components

Hidden Layer Transformation: $h = \tanh(W \cdot \text{concat}(\text{embeddings}) + b)$

tanh activation: Provides non-linearity, bounded output [-1,1]
Concatenation: Treats context as one big feature vector
Weight sharing: Same $W$ for all positions

Output Layer:

\[\text{logits} = U \cdot h + d\] \[P(\text{word} | \text{context}) = \text{softmax}(\text{logits})\]

Training Dynamics: Where the Magic Happens

Backpropagation Flow:

Loss computation: Cross-entropy between predicted and actual next word
Output layer gradients: Standard softmax gradients
Hidden layer gradients: Backprop through tanh
Embedding gradients: 🎯 This is where the magic happens!

Embedding Update Intuition:

Words in similar contexts get pulled together
Words in different contexts get pushed apart
Smooth interpolation emerges in embedding space

Experimental Results & Revolutionary Impact

Performance Breakthroughs

Penn Treebank Results:

Traditional trigram: ~170 perplexity
Bengio’s model: ~109 perplexity
🚀 35% improvement in perplexity!

What is Perplexity?
Perplexity measures how “surprised” a language model is by test data. If perplexity = 100, the model is as uncertain as if it had to choose uniformly among 100 words. Lower perplexity = Better model.

Qualitative Discoveries

Learned Word Clusters:

Numbers: one, two, three, four…
Days: Monday, Tuesday, Wednesday…
Verbs: running, walking, jumping…
Animals: cat, dog, horse, bird…

The Limitations That Sparked Future Research

1. The Softmax Bottleneck

The Problem: $P(w_t | \text{context}) = \frac{\exp(\text{score}(w_t))}{\sum_{w \in V} \exp(\text{score}(w))}$

Computing this requires

forward passes for normalization!

Solutions (developed later):

Hierarchical Softmax (Morin & Bengio, 2005)
Negative Sampling (Mikolov et al., 2013)
Noise Contrastive Estimation (Mnih & Teh, 2012)

2. Fixed Context Window

Only looks at $n-1$ previous words
Can’t capture long-range dependencies
Solution: RNNs, LSTMs, eventually Transformers

3. Sequential Processing Bottleneck

Must process words one by one
No parallelization during training
Solution: Attention mechanisms, Transformers

Historical Context: The Lineage of Ideas

What Came Before

Shannon (1948): Information theory foundations
Brown et al. (1992): Statistical language modeling
Kneser-Ney (1995): Sophisticated smoothing

The Direct Lineage

timeline
    title Evolution of Neural Language Models
    2003 : Bengio's Neural LM
         : Distributed word representations
    2013 : Word2Vec
         : Simplified embedding learning
    2014 : GloVe
         : Global vector representations
    2017 : Transformer
         : Self-attention revolution
    2018 : BERT/GPT
         : Pre-trained language models
    2022 : ChatGPT
         : Conversational AI breakthrough

Modern Perspective: What We Learned

1. Embeddings Are Universal

Key Insight: Any discrete symbol can be embedded in continuous space

Vision: Patch embeddings in Vision Transformers
Audio: Learned audio representations
Code: Code embeddings for programming languages
Molecules: Chemical compound embeddings

2. Scale Changes Everything

Bengio’s Scale (2003):

Vocabulary: ~17k words
Embeddings: 30-100 dimensions
Hidden units: 50-200

Modern Scale (2024):

Vocabulary: 50k+ tokens
Embeddings: 768-12,288 dimensions
Parameters: Billions to trillions

3. The Architecture Evolution

Bengio’s insight + Modern architectures:

Component	Bengio (2003)	Modern Evolution
Context	Fixed n-gram window	Global attention (Transformers)
Processing	Sequential	Parallel processing
Memory	No memory	Long-range dependencies
Scale	Thousands of params	Trillions of parameters

Why This Paper Is Foundational

1. The Paradigm Shift

Before: Language is discrete symbols + statistics
After: Language is continuous geometry + learning

2. Unified Framework

This paper showed that neural networks could learn language structure without hand-crafted features. This insight scales to:

Translation: Encoder-decoder architectures
Question Answering: Reading comprehension models
Generation: GPT-style autoregressive models

3. Philosophical Impact

Distributed Representations: The idea that meaning emerges from patterns in high-dimensional space has influenced:

Cognitive Science: How brains might represent concepts
AI Safety: Understanding model representations
Interpretability: Probing what networks learn

Implementation Insights

Key Design Decisions Explained

Why concatenation instead of averaging?

Preserves positional information
Allows learning position-specific patterns
More expressive than simple averaging

Why tanh activation?

Bounded output prevents exploding gradients
Smooth gradients for better optimization
Zero-centered unlike sigmoid

Why this specific architecture?

Feedforward: Simpler than RNNs (which barely worked in 2003)
Single hidden layer: Computational constraints of the era
Fixed window: Tractable optimization

The Comparison Matrix

Method	Strengths	Weaknesses	Perplexity (Penn Treebank)
N-gram + Kneser-Ney	Fast, interpretable	No generalization, sparse	~170
Bengio Neural LM	Generalization, embeddings	Slow training, fixed window	~109
Modern Transformers	Long context, parallelizable	Massive compute requirements	~20-50

The Legacy: From 2003 to ChatGPT

Direct Descendants

Word2Vec (2013): Simplified Bengio’s approach, focused only on embeddings
GloVe (2014): Global statistics + local context
ELMo (2018): Contextualized embeddings
BERT (2018): Bidirectional encoder representations
GPT (2018+): Autoregressive generation at scale
ChatGPT (2022): Conversational AI built on these foundations

The Fundamental Insight That Persists

Every modern language model uses Bengio’s core insight:

Words are points in continuous space where meaning emerges from geometric relationships

Conclusion: The Paper That Changed Everything

Bengio’s 2003 paper wasn’t just a technical contribution—it was a conceptual revolution. The idea that we could learn continuous representations of discrete symbols fundamentally changed how we think about language and meaning.

The revolution wasn’t just neural networks for language—it was learning continuous representations of discrete symbols.

Today, when you ask ChatGPT a question, when Google Translate converts text between languages, when your phone’s autocomplete suggests the next word—you’re witnessing the legacy of this single paper.

Key Takeaways:

🧠 Distributed representations are more powerful than discrete symbols
🎯 Neural networks can learn language structure automatically
📈 Geometric relationships in embedding space capture semantic meaning
🚀 Generalization comes from continuous interpolation between examples

The next time someone talks about “embeddings” or “neural language models,” remember: it all started with Bengio’s simple but revolutionary idea that words could be points in space.